「MATLAB FBX LoaderとMATLAB 3D Model Rendererの開発」
の記事です.
担当はrej55です.
前半はMATLAB FBX Loaderについて,後半はMATLAB 3D Model Rendererについて書いています.
まえがき
近年,3DCGの技術が大きく発達してきているなと感じています.今年のAdvent Calenderでもisskくんの記事やLineaくんの記事などで綺麗なグラフィックスが載っています.彼らといろいろと話をしていて,自分も3DCGに興味を持ったのでどこかで勉強してみたいと思っていました.
私はMATLABを利用したプログラミングが大好きで,東工大では学生が無料でMATLABを使用できるという背景もあり,趣味でいろいろと開発をしていました.今回は,MATLABで3DCGの描画ができないか?ということで試してみることにしました.
MATLAB FBX Loaderとは?
FBXファイルとは,3Dデータを異なるアプリケーション間でやり取りできるように設計されているファイルのことで,Autodesk社によって開発されています.MATLAB FBX Loaderは,MATLABでこのFBXファイルを読み込むためのライブラリとなります.
MATLAB FBX LoaderではFBXファイル内に格納されている情報を出力します.具体的には,
- 頂点の数
- 頂点の3D座標
- ポリゴンを構成する頂点の集合
- 各頂点のUV座標
- 各頂点の法線ベクトル
- 各頂点のカラーデータ
FBX Loaderの開発
FBXファイルはバイナリ形式のファイルなので,基本的にフォーマットがわかっていないと読み込むことが不可能です.MATLABでもバイナリファイルの読み込みは可能なのですが,そもそもフォーマットがわかっていないので読み込みができません.
実は,Autodesk社のほうでFBXファイルの読み込みなどができるSDKを配布しています.このFBX SDKはC++とPythonのものしかなく,そのままではMATLABでは使えません.そこで今回はMEXというものを介してFBX SDKを利用することを考えました.
MEXについて
MEXとは,MATLAB上でCやC++で開発された関数を呼び出すための機能で,CおよびC++コードをMEXファイル生成用にコンパイルするとMATLABで関数を呼び出すことができるようになります.
MEXファイルの作成にあたっては,まず下記のようなmexFunctionを用意します. mexFunctionはMATLABがMEXファイルを呼び出したときに実行されるゲートウェイ関数です.基本的にこのmexFunction内で処理を記述します.
MATLAB FBX Loaderは,FBX SDKのAPIを呼び出し,FBXファイル内の必要なデータをひたすらMATLABに出力として渡すという処理を書いているものになります.FBX SDKの詳細についてはこちらとこちらを参考にさせていただきました.
MATLAB 3D Model Rendererとは?
MATLAB 3D Model Rendererは,MATLAB FBX Loaderで読み込んだ3Dモデルのデータを元に3DCG画像を生成するシステムです.GPUのハードウェア機能を直接使っているわけではないので,いわゆるソフトウェアレンダラに分類されるかと思います.
MATLAB 3D Model Rendererのパイプラインは下記のとおりです.
- ワールド座標からビュー座標への変換
- ビュー座標からスクリーン座標への射影
- スクリーン座標データを元にラスタライズ
- テクスチャフェッチ
ワールド座標からビュー座標への変換
この節では,ワールド座標上の3Dモデルをカメラから見たビュー座標系に変換する方法を説明します. ワールド座標とは,3Dモデルの3D空間上での物体の位置を表す絶対座標系です.ビュー座標系は,カメラの位置を原点として,視点方向ベクトルとカメラの上方向ベクトルとこの2つに直交するベクトルを基底とする座標系です.
まず,ビュー座標系の基底ベクトルを求めます.ビュー座標系の基底ベクトルはカメラの視線方向の単位ベクトル$c_t$,カメラの上方向単位ベクトル$c_u$,カメラの右方向の単位ベクトル$c_r$です.これらは下記のように求めます. $$ c_t = \frac{x - t}{\| x - t \|},\ c_u = \frac{c_t \times u}{\|c_t \times u\|},\ c_r = c_t \times c_r $$ ここで,$x$はカメラのワールド座標における位置,$t$は注視点,$u$はカメラの上方向を表すベクトルです. これらの基底ベクトルを利用して,下記のような同次座標変換行列を定義します. $$ T_{\mathrm{view}} = \begin{bmatrix} c_t^{\sf T} & -c_t^{\sf T} x\\ c_u^{\sf T} & -c_u^{\sf T} x\\ c_r^{\sf T} & -c_r^{\sf T} x\\ O & 1 \end{bmatrix} $$ この行列により座標変換を行うことで,ワールド座標からビュー座標への変換が完了します.具体的なソースコードは下記のようになります.
ビュー座標からスクリーン座標への射影
スクリーン座標はその名の通りスクリーン上における2次元の座標系です.ここでは,最も簡単なピンホールカメラモデルに基づいて,ビュー座標系で表される3次元空間上の頂点をスクリーン上の座標へ射影したいと思います.
カメラとスクリーンの距離を$f$とすると, $$ P_{\mathrm{screen}} = \begin{bmatrix} -f & & &0\\ & -f & &0\\ & & 1 &0 \end{bmatrix} $$ が射影変換行列となります.これを用いて,ビュー座標系における頂点の座標は下記のように射影されます. $$ \begin{bmatrix} U \\ V \\ S\end{bmatrix} = P_{\mathrm{screen}} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix} $$ 上記の処理は下記のように実装できます.
ラスタライズ
画像を生成するためには,座標データからピクセルのデータに変換する必要があります.この変換処理のことをラスタライズと呼びます.
ラスタライズを行うために,まず画像の各ピクセルとスクリーンの座標の対応を求めます.この処理は,meshgrid関数を利用すると簡単に求めることができます.MATLABでは画像データを行列形式で扱います.行列の各要素が各ピクセルの画素値に対応します.ここで, [X, Y] = meshgrid(linspace(-width, width, w_res), linspace(height, -height, h_res))とすると, XとYは画像の解像度と同じサイズの行列となり,Xには各ピクセルのスクリーン上における$x$座標,Yには$y$座標といったデータが入るため,このXとYを利用することで各ピクセルのスクリーン上における座標を得ることができます.なお,Y座標を反転させているのは,上記のピンホールカメラモデルでスクリーンへ投影すると上下反転した状態で投影されるからです.
ラスタライズを行うためには,各ポリゴンの内部を塗りつぶす処理が必要になります.そのためには,頂点データから多角形の内部判定を行う必要があります.多角形の内部判定を行う関数として,MATLABにはinpolygonという関数があり,これを利用すると各クエリ点が多角形の内部または境界上にあるかを判定することが可能です.
テクスチャフェッチ
ポリゴンをラスタライズする際に,どの色を割り当てるのかという問題が生じます.このとき,UV座標とテクスチャファイルが割り当てられていれば,頂点のUV座標をもとにしてポリゴンの中にテクスチャ画像に対応する色を付けることができます.この処理のことをテクスチャフェッチと呼びます.UV座標についてはこちらの解説を参考にさせていただきました.
UV座標は頂点に割り当てられているため,頂点に対応する各ピクセルのUV座標を求め,ポリゴン内部のピクセルのUV座標を求める必要があります.具体的には,頂点のスクリーン座標におけるUV座標から,各ピクセルの座標におけるUV座標を内挿する計算を行います.このような内挿は,scatteredInterpolantという関数を利用することで内挿のための関数のようなものを求めることができます.実際は,ポリゴンの外側のUV座標を計算するのは無駄なので,ポリゴンの内部のピクセルだけ計算することで計算の高速化を行います.また,隠れた面を描画しないようにするために,各頂点がスクリーンからどの程度離れているかを表すデプスの計算も行います.この計算も,各頂点のスクリーン座標に対するスクリーンからの距離をもとに各ピクセルにおけるデプス値を内挿するように行います.
上記のラスタライズおよびテクスチャフェッチを実装すると下記のようになります.
実際に試してみよう
今回は例としてユニティちゃんを表示してみたいと思います.
実行した結果がこちらです.

ジャギーを少し軽くするため,上記の処理に加えて今回は出来た画像に対しガウシアンフィルタで軽く平滑化をかけています.
続いて,背景画像と一緒に全身を表示してみます.
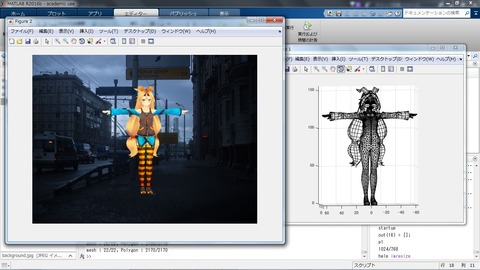
背景画像を初期値に指定すれば,3Dモデルを上から塗り重ねるようにしてレンダリングすることができます.
まとめ
長くなってしまいましたが,MATLABでFBXを読み込む方法とMATLABで3Dモデルをレンダリングする方法について書きました.いかがでしたか?
レンダリング自体はかなり計算時間がかかるため,正直なところリアルタイムには向いてないと思います.ですので,現状のままではMATLABで3Dゲームを作る,みたいなものは非常に厳しいと思います.なお,レンダリング処理はGPUを利用することで高速化できますが,これでもリアルタイムには厳しいといったところです.
基本的な描画が可能になったので,今後は下記のような課題が考えられます.
- 光源の影響を計算するシェーディング処理
- カメラのボケなどを再現するエフェクト処理
私の記事は以上となります.明日はPLM_precure氏の「ジープがお好き?結構。ではますます好きになりますよ。」の記事となります!